Quote:
Originariamente inviata da zicchinet
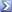
50,0mL di una soluzione di Ca 2+ 0,0400M (tamponata a pH 10,00) è titolata con EDTA 0,0800M. Calcolare il pCa2+ al punto di equivalenza utilizzando la costante di formazione condizionale K ' f (la costante di formazione K f per CaY 2- =4,9x10 10 ) ( a 4 a pH 10=3,5x10 -1 )
|
effetivamente i dati sono scritti in modo abbastanza incomprensibile..ma ci provo cmq:
al p.eq. deve essere
50.0mL * 0.0400M = V(EDTA) * 0.0800M
=> V(EDTA) = 50.0mL*0.0400M / 0.0800M = 25mL
=> al p.eq V finale = 50+25 = 75mL
=> la conc. tot di Ca = 0.0400M*50.0mL / 75mL = 0.0267M
Ca++ + Y---- <-- --> CaY--
Kf = [CaY]/[Ca]*[Y]
=> [CaY] = Kf*[Ca]*[Y]
0.0267 = [Ca]+[CaY] =
= [Ca]+Kf*[Ca]*[Y] =
= [Ca]*{Kf + [Y]}
=> [Ca] = 0.0267 / {Kf + [Y]}
Non resta che trovare [Y----]:
crdo che tu volessi scriver la Ka4 dell'EDTA:
HY--- <-- --> H+ + Y----
Ka4 = [H+][Y]/[HY] = 3.5*10^-1 vero?
=> [HY] = [H+]*[Y]/Ka4
EDTA tot sarà = 0.0800M * 25mL / 75mL = 0.0267 (siamo al p.eq!!!!)
=> 0.0267 = [Y]+[HY]+ [CaY]=
= [Y]+[H+]*[Y]/Ka4 + Kf*[Ca]*[Y]
= [Y]*{1 + [H+]/Ka4 + Kf*[Ca]} =
= [Y]*{1 + [H+]/Ka4 + Kf*0.0267 / {Kf + [Y]}
dove [H+] = 10^-pH = 10^-10
quindi hai da svolgere questa equazione:
0.0267 = [Y]*{1 + 10^-10/(3.5*10^-1) + 4.9*10^10*0.0267 / {4.9*10^10 + [Y]}
dopo che hai trovato [Y]
puoi calcolarti [Ca] e quindi pCa
(non me ne volere, ma non ho tempo di svolgere tutti i calcoli...)