Quote:
Originariamente inviata da zicchinet
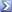
50,0mL di una soluzione di Ca 2+ 0,0400M (tamponata a pH 10,00) è titolata con EDTA 0,0800M. Calcolare il pCa2+ al punto di equivalenza utilizzando la costante di formazione condizionale K ' f (la costante di formazione K f per CaY 2- =4,9x10 10 ) ( a 4 a pH 10=3,5x10 -1 )
|
-Al punto di equivalenza le moli di Ca++ sono uguali alle moli di EDTA (=acido etilendiamminotetraacetico, che lega stabilmente cationi bivalenti). Quindi si può scrivere l'ugualglianza:
nCa++ =
n EDTA
Non abbiamo le moli, però si possono ricavare, e si riscrive l'uguaglianza:
MCa++ x
VCa++ =
M EDTA x
V EDTA
L'unica incognita, in questa uguaglianza (nota: NON è una proporzione!!) è il V di EDTA, che dunque potrà essere calcolato:
V = M Ca x V Ca / M EDTA = 25 ml
-Inizialmente il volume era di 50 ml (da traccia); ad essi si aggiunge il volume di EDTA, per cui il volume finale diventa:
V= 50 + 25 = 75 ml
-Si calcola ora la concentrazione di Ca++ fianle, facendo la seguente proporzione:
0,0440 : 75 = (Conc. di Ca++) : 50
Da questo calcolo, si ottiene una concentrazione di Ca++ pari a 0,0266
-Per qualsiasi rezzione all'equilibrio, si può scrivere la formula della costante. Quindi, se l'equilibrio è:
Ca++ + Y --> CaY
si può scrivere la Kf (che nel nostro quesito ha un valore noto):
Kf = [CaY] / [Ca++] x [ Y]
Da tale formula, si ricava la [CaY]:
[CaY]= Kf x [Ca++] x [Y]
- Ora, dai calcoli precedenti, risulta noto che la quantità totale di Calcio è di 0,0266, che si può scrivere così:
[Ca] +
[CaY] = 0,0266
(Ma poichè
[CaY]= Kf x [Ca++] x [Y], si può scrivere anche):
[Ca] +
Kf x [Ca++] x [Y] = 0,0266
Si mette [Ca] in evidenza e si ottiene:
[Ca] x (Kf + [y]) = 0,0266
-Si calcola la [Ca] , poichè tutti i valori sono noti:
[Ca] = 0,0266 / (Kf + [y])
-A questo punto, con una serie di passaggi matematici, ci si può calcolare Y.
-Infine si calcolerà la [Ca] con la formula su scritta:
In bocca al lupo!
Dott.ssa Raffaella Russo
[Ca] = 0,0266 / (Kf + [y])